B 트리
목차
B트리와 B+ 트리
정보처리기사를 공부하다 데이터베이스 인덱스에서 B트리 및 B+트리를 왜 사용하는지 궁금해서 검색해보았다.
일반적인 이진 탐색 트리의 경우 트리가 한쪽으로 쏠릴 경우 O(N)의 시간 복잡도를 가지게 되는데, 이를 해결하기 위해 자가 균형 이진 탐색 트리 (AVL 트리, RB(Red-Black) 트리) 라고 삽입/삭제 시 트리의 균형을 맞춰주는 트리가 셜계되었다.
그중에서 왜 데이터베이스 인덱스를 관리할 때에는 주로 B트리 및 B+ 트리를 사용하는지에 대해 알아보자.
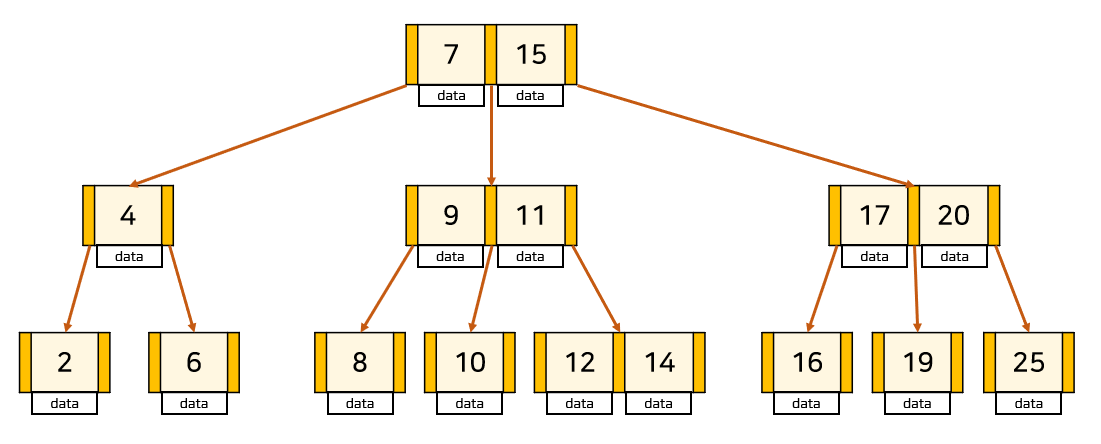
B 트리의 검색 / 삽입(갱신) / 삭제
B+ 트리
B 트리와 B+ 트리의 차이 및 DB 인덱스에서 B+트리를 사용하는 이유
요약 : 다른 자가 균형 이진 탐색 트리 및 B 트리를 데이터베이스 인덱스에서 사용하지 않는 이유
-
=등호 연산 뿐만 아니라< >부등호 연산도 지원해야 하기 때문.-
< >연산을 지원하기 위해 다른 가지를 재접근/탐색해야 하기 때문. (이때문에 B트리도 잘 사용되지 않는다. B+ 트리는 리프노드에서 연결리스트로 이동만 하면 되기 때문에 빠름)예를 들어 아래와 같은 사진에서 14와 같거나 크고 16보다 작거나 같은 데이터 (`WHERE data >= 14 AND data <= 16`)를 찾는다고 가정해 보자.
일반적인 B트리의 경우 14, 15, 16을 찾기 위해 14노드에 접근 후 15 노드로 이동 후 16노드까지 이동하여 데이터를 찾아야 한다.
B+ 트리의 경우 14노드에 접근 후 연결리스트 포인터를 통해 15 ~ 16을 바로 찾을 수 있기 때문에 불필요한 노드 간 이동이 없어 보다 효율적이다.
-
- 참조 포인터가 적어 수많은 데이터를 빠르게 접근할 수 있음.
- 데이터 탐색 뿐 아니라 삽입/수정/삭제를 통한 트리 재구성이 필요한 경우에도 항상 동일한 시간복잡도 (O(logN))을 가짐.
사실 등호 연산의 경우에는 B+ 트리보다 B트리가 좀 더 빠를 수 있고 (B+트리는 무조건 리프 노드에서 찾아야 하지만 B트리는 브랜치 노드(가지 노드) 에서도 찾을 수 있기 때문에) 해쉬 테이블의 경우 O(1) 의 시간 복잡도를 가지기 때문에 훨씬 빠르겠지만 DB 참조의 경우 < > 연산 또한 많이 사용되기 때문에 B트리 및 해쉬테이블이 비효율적일 수 있다.